La Magia del numero 6174 13 Novembre 2023 – Posted in: Lo Sapevi che – Tags: #CostanteDiKaprekar #Numero6174 #MagiaDellaMatematica #CuriositàMatematiche #Kaprekar #MatematicaIntrigante #MatematicaDivertente #ScoperteNumeriche #EducazioneMatematica #AmorePerLaMatematica, #curiosity, #fenomenologia, #matematica, #好奇心, #語言現象學, curiosité, curiosities, curiosity meaning, did you know that, Kaprekar, lo sapevi che, mathematics, Neugier, Phänomenologie, Phänomenologie der Sprache, phénoménologie, phénoménologie du langage, saviez-vous que, wusstest du das, अंक शास्त्र, क्या आप जानते हैं, घटना phenomenology, जिज्ञासा, भाषा की घटना विज्ञान phenomenology of language, 你知道嗎 Curiosità, 現象學 Fenomenologia della lingua
La Magia del 6174: esplorando la Costante di Kaprekar
Nel mondo dei numeri e delle loro infinite curiosità, la “costante di Kaprekar” emerge come un fenomeno affascinante. Scoperta dal matematico indiano D.R. Kaprekar, questa costante – il numero 6174 – rivela un aspetto quasi magico delle operazioni matematiche.
Dattaraya Ramchandra Kaprekar (1905–1986) era un insegnante indiano di matematica. Pur non avendo una specializzazione accademica, fece molte scoperte nella teoria dei numeri, tra i quali una costante e una classe di numeri che da lui hanno preso il nome, divulgati attraverso una serie di articoli su riviste di modesto prestigio scientifico.
Si occupò anche di quadrati magici e matematica ricreativa. Studioso solitario e poco apprezzato dai colleghi indiani, diventò famoso quando Martin Gardner nel 1975 si occupò di lui in un articolo della rubrica Mathematical Games che teneva sullo Scientific American.
In questo articolo, ci immergeremo nella scoperta di Kaprekar e esploreremo perché il numero 6174 è così speciale.
Cos’è il Numero 6174?
Il numero 6174 è noto per la sua singolare proprietà nella matematica: se prendi qualsiasi numero a quattro cifre (dove non tutte le cifre sono uguali, i cosiddetti numeri a cifra ripetuta come 1111), riordini le cifre in ordine crescente e decrescente, e sottrai il numero minore da quello maggiore, ripetendo questo processo, finirai per arrivare al numero 6174 in un massimo di sette iterazioni.
Una volta raggiunto, il processo si blocca in un ciclo continuo che riporta sempre al 6174.
Esempio Pratico
Prendiamo ad esempio il numero 3524: 1. 5432 – 2345 = 3087 2. 8730 – 0378 = 8352 3. 8532 – 2358 = 6174 Da questo punto, ogni iterazione ti riporterà al 6174: 4. 7641 – 1467 = 6174
Perché è Importante?
Questa costante non è solo un trucco matematico, ma una dimostrazione della capacità della matematica di rivelare schemi e ordini inattesi. Il 6174 agisce come un “punto fisso” in questo particolare processo, sottolineando la stabilità e la prevedibilità nascoste nelle operazioni numeriche.
La Costante di Kaprekar nell’Insegnamento
Nell’educazione matematica, la costante di Kaprekar può essere utilizzata per stimolare la curiosità e l’interesse degli studenti. È un esempio eccellente di come la matematica, spesso vista come astratta e complessa, possa essere allo stesso tempo accessibile e intrigante.
Il Contributo di D.R. Kaprekar
D.R. Kaprekar, un matematico autodidatta, ha lasciato un segno indelebile nel mondo della matematica con questa e altre scoperte. La sua passione e dedizione alla matematica offrono un esempio ispiratore di come la perseveranza e la curiosità possano portare a scoperte significative.
Conclusione
La Bellezza Nascosta nei Numeri
La costante di Kaprekar ci mostra che anche nelle operazioni più semplici possono celarsi meraviglie matematiche. Questo non solo arricchisce la nostra comprensione della matematica, ma invita anche a riflettere sulla bellezza e sui misteri nascosti nei numeri che ci circondano nella vita quotidiana.
Con il numero 6174, Kaprekar ha svelato un angolo sorprendente del mondo numerico, dimostrando che la matematica può essere fonte di stupore e ammirazione continua.
Curiosità
E se le cifre del numero non sono quattro? Lo stesso Kaprekar scoprì che un numero di due cifre non converge verso un solo valore, ma si impantana nel loop 9→81→63→27→45→9. Le cose cambiano con tre cifre: l’operazione questa volta converge verso un solo valore, il numero 495. Ad esempio, prendiamo 586. In ordine decrescente le cifre danno 865 e in ordine crescente danno 568.
865 – 568 = 297.
972 – 279 = 693.
963 – 369 = 594
945 – 459 = 495
945 – 459 = 495.
Con le cifre 4, 5 e 9 la cifra finale sarà sempre 495.
Attraverso lo stesso procedimento usato per il caso delle quattro cifre e del numero 6174, si può dimostrare che 495 è l’unica soluzione possibile per un numero di tre cifre.
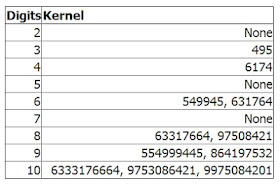
Per numeri con un numero di cifre superiore a 4 si è scoperto quanto riportato nella tabella, sempre fornita da Yutaka Nishiyama:
© copyright 2023 – tutti i diritti sono riservati.