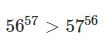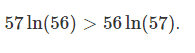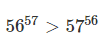Quale numero è più grande? 16 Luglio 2022 – Posted in: Momento Ludus – Tags: #matematica, derivata, fenomenologia della matematica, indovinello matematico, momento ludus, numeri, quale numero è più grande
Indovinelli matematici : quale numero è più grande: 56^(57) oppure 57^(56)?
La disciplina della matematica è una delle più difficili in assoluto. Una disciplina “ostica” non per tutti, una materia che con il corso degli anni si è evoluta, sempre di più diventando a detta di molti sempre più difficile. Come renderla più gradevole e meno frenante? Divertendo! Sono così nati gli indovinelli matematici, una vera risorsa per avvicinarsi alla materia.
Ovviamente senza applicazione e studio si fa poca strada ma esistono molti metodi che vi permettono di impararla come si deve.Avete mai sentito parlare fino ad oggi di indovinelli matematici? Siamo sicuri di sì. Proseguendo nel nostro articolo, cominceremo con la collaborazione della Prof.ssa Melissa che da anni insegna in ogni ambito didattico e assume proprio come cavallo di battaglia, come chiave di apprendimento della materia, il metodo “divertente” e pratico. Con lei vedremo una lista dettagliata dei migliori enigmi da risolvere utilizzando le proprie basi. Capacità di logica e di matematica, dal più semplice al più complicato in assoluto, alcuni con dei trabocchetti a cui stare molto attenti.
Ad ogni modo, sono tutti con soluzioni e spiegazione finale dettagliata, in modo da aiutarvi a capire come mai la soluzione sia quella.
Un’utile palestra per poter allenare nel miglior modo possibile la propria abilità. Un buon metodo per tenere in allenamento la mente cosi da applicarvi il più possibile in una materia difficile come la matematica. Il cervello abbisogna di costante allenamento e con il tempo i risultati non tarderanno ad arrivare!
“Uno degli aspetti infinitamente seducenti della matematica è che i suoi paradossi più spinosi trovano la via di fiorire in splendide teorie.” (Philip J. Davis)
Forza cominciamo ad allenarci!
L’affermazione :
è equivalente a
Prendendo il quoziente otteniamo che questo equivale a
Definire la funzione:
La sua derivata è
che è negativa per
Pertanto la funzione ϕ diminuisce su
Dal momento che
otteniamo
Per l’equivalenza precedentemente dimostrata abbiamo che il numero più grande è:
Due lezioni che vorrei trasmettere:
- Per dimostrare le uguaglianze o le disuguaglianze è bene usare le equivalenze. Funzionano molto più semplicemente che le uguaglianze.
- Quando uno ha una disuguaglianza complessa come quella da dimostrare, vale la pena semplificarla prima di passare a tecniche standard come la derivata.
© copyright 2022 – tutti i diritti sono riservati.